
One of the most well-known books from India, the country where I was born, is a 2000 year old text called The Kama Sutra. In it, there is a chapter that describes how lovers can exchange secret messages using a simple encryption technique. The method described is a substitution cipher, where each letter in the message is substituted with another letter using a formula known only to the sender and the receiver. While the book is famous or infamous for being a sex manual, it should be equally famous for containing one of the oldest known descriptions of encryption in history.
By 900AD, Arab mathematicians had worked out how to crack substitution ciphers by analyzing the frequency and position of the letters. Over the years scientists have come up with more and more sophisticated encryption techniques, such as, for example the widely used RSA encryption. The RSA protocol is based on finding the factors of a large number, a task that is provably difficult to accomplish. However, with enough computing one could do it and therefore hack RSA encryption.
Quantum physics provides a completely different way to approach encryption by harnessing the fundamental laws of physics itself. A key ingredient of quantum encryption is the Heisenberg uncertainty principle, which states that one cannot precisely know every property of a quantum object such as an electron or a photon. For example, if the position of a particle is precisely known, then its momentum is completely unknown, and vice versa. This uncertainty is not due to limitations in our measurement devices but is built into the theory itself. One cannot simultaneously know every property of a quantum object because it is fundamentally unknowable. The modern quantum information revolution is based on a revolution in how we think of strange quantum ideas such as uncertainty. Scientists have come to realize that strange quantum properties are not a hindrance but are in fact a powerful resource for information processing applications.
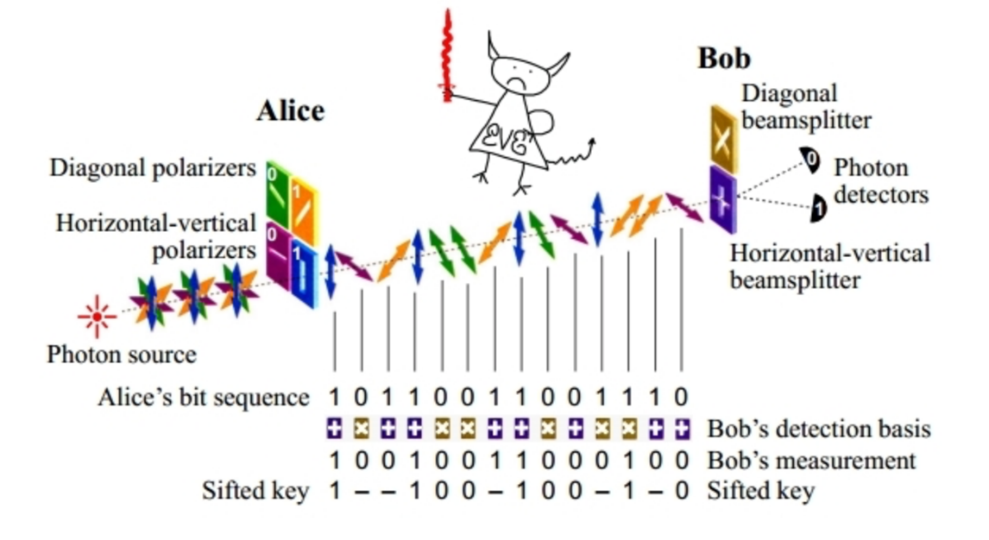 Quantum uncertainty can be used for encryption by hiding information from an eavesdropper Eve. Let’s say Alice sends a secret key to Bob encoded in a string of quantum particles such as photons. Each photon encodes a single bit of the key – a 0 or 1. If Eve tries to steal the photons during transmission, read the bits and then replace the photons with identical ones to hide her presence, quantum uncertainty will prevent her from precisely duplicating each photon. By checking a few of the photons for tampering, Alice and Bob will always be able to detect Eve’s presence. If they suspect that she has been listening in, they discard the key and start again until they are satisfied that it is untampered. This is the only known perfectly unhackable method for generating a secret key. After all Eve would have to violate the laws of physics in order to escape quantum uncertainty and hack the key. Most importantly, future improvement in Eve’s computational power or resources, and even access to a quantum computer, will not increase her ability to violate quantum uncertainty and break the encryption.
Quantum uncertainty can be used for encryption by hiding information from an eavesdropper Eve. Let’s say Alice sends a secret key to Bob encoded in a string of quantum particles such as photons. Each photon encodes a single bit of the key – a 0 or 1. If Eve tries to steal the photons during transmission, read the bits and then replace the photons with identical ones to hide her presence, quantum uncertainty will prevent her from precisely duplicating each photon. By checking a few of the photons for tampering, Alice and Bob will always be able to detect Eve’s presence. If they suspect that she has been listening in, they discard the key and start again until they are satisfied that it is untampered. This is the only known perfectly unhackable method for generating a secret key. After all Eve would have to violate the laws of physics in order to escape quantum uncertainty and hack the key. Most importantly, future improvement in Eve’s computational power or resources, and even access to a quantum computer, will not increase her ability to violate quantum uncertainty and break the encryption.
Things get even more interesting when two or more particles interact. Quantum particles can get locked together in a powerful connection called entanglement. Like pairs of gloves or socks, the quantum particles are perfectly matched, but individually they each still obey the law of uncertainty and do not have a precise identity. In the language of quantum information, one can describe an entangled pair as both particles being 0 or both particles being 1, but due to uncertainty, there is no way to know whether each individual particle is a 0 or a 1. There is some possibility that an individual particle is 0 and some possibility that it is 1. What is certain is that if one particle is 0 then so is the other and vice versa. This balance of perfect joint correlation and individual uncertainty is a novel phenomenon that can be harnessed for new communication protocols. For example, the information encoded in a particle such as a photon can be teleported from Alice to Bob without physically sending the photon, provided Alice and Bob each have one particle of an entangled pair. Thanks to the connection between the entangled particles, Alice and Bob can manipulate their individual particles in such a way that the information in the photon is erased on Alice’s end and reconstructed on Bob’s end.
My research team is currently working to analyze and characterize multipartite entangled networks and their applications for quantum information processing. We have developed new techniques to measure entanglement and to purify entanglement in realistic optical systems. We also design and analyzed novel protocols such as quantum voting and multiparty teleportation, not only for better information processing, but also to gain insight into the nature of quantum behaviour and its difference from our familiar classical world.
Quantum physics had already transformed society. It has led to the laser and transistor and all of our modern technologies today. We are now on the brink of the second quantum revolution as we begin to harness all of the power of the quantum world. Quantum information processing will not only transform communication and security, but will impact healthcare, climate modeling, scientific research and machine learning. It’s my hope that together with this new quantum revolution, we have a revolution in inclusivity, equity and diversity in the physics community so that all contributions will be supported and encouraged and we can jointly embark on this exciting journey of discovery.
Shohini Ghose is a theoretical physicist whose pioneering work in the field of quantum information science and quantum chaos has helped shape the field. She has received numerous awards and recognitions for her scientific breakthroughs, is an internationally sought-after public speaker, and a TED fellow. She also makes a local, national and international impact as the founding Director of Laurier’s centre for Women in Science, the first of its kind in Canada

